Sensing Systems for Respiration Monitoring: A Technical Systematic Review

Dale3/19/25

What is Kalman Filter?

A recursive way to compute conditional expectation.

(The KF was discussed in page 47-48 of the paper.)

Kalman filter: This technique has been used by several studies as a sensor fusion method. Thus, it is not a method to extract breathing parameters but to fuse measurements from different sensors. When multiple respiration sensors are available, the measurements they provide are not exactly the same. Furthermore, measurements always contain noise. The Kalman filter is used to provide a final value based on the measurements of the different sensors, the model of variation of the breathing parameter, the noise model of the sensors, and the variation model [270]. Figure 33 shows an overview of the Kalman filter algorithm adapted to the fusion of breathing sensors

The Kalman filter has two distinct phases: prediction and update. The prediction phase estimates the state (breathing parameter) in the current time step using the state estimate from the previous time step (previous breathing parameter). The breathing parameter predicted in this phase is called the “a priori” state estimate $\hat{x}_{k|k-1}$ and is obtained according to Equation (26):

\hat{x}_{k|k-1} = A \hat{x}_{k-1|k-1}

where $\hat{x}_{k-1|k-1}$ is the state estimate in the previous state, in this case the previous breathing parameter estimated, and $A$ is the state transition model.

Ask GPT

在卡尔曼滤波器的文献中， $\hat{x}_{k|k-1}$ 和 $\hat{x}^{-}_k$ 通常表示相同的概念，即“先验”状态估计。

Matrix $A$ represents the expected evolution of $\hat{x}_{k-1|k-1}$ for the next transition. As breathing does not vary much in the short term [102], a common approach is to define $A$ as an identity matrix, so the “a priori” state estimate $\hat{x}_{k|k-1}$ is equal to the previous state $\hat{x}_{k-1|k-1}$ . If respiration is not expected to be constant in the short term, $A$ should contain the linear variation model. The “a priori” estimate covariance $P_{k|k-1}$ (Equation (27)), which is a measure of the accuracy of the “a priori” state estimate $\hat{x}_{k|k-1}$ , must also be predicted. It depends on the transition model $A$ , the value of the covariance in the previous transition $P_{k-1|k-1}$ , and $Q$ . $Q$ is the covariance of the process noise (the noise of $\hat{x}_{k|k-1}$ prediction model). In order to apply the Kalman filter, the process noise must follow a Gaussian distribution with zero mean and covariance $Q_k \sim \mathcal{N}(0, Q)$ . Although $A$ and $Q$ can vary at each time step $k$ , it is common for them to take a constant value. Many methods exist to determine $Q$ . In the breathing system presented by Yoon et al. [131], $Q$ was a diagonal matrix (which is a common approach) of the order of $10^{-4}$ .

P_{k|k-1} = A P_{k-1|k-1} A^T + Q. \quad (27)

Ask GPT

PQ矩阵用于描述卡尔曼滤波器中的误差协方差和过程噪声：

$P$ ：误差协方差矩阵，描述状态估计误差的协方差。它在预测和更新阶段都会被更新。
$Q$ ：过程噪声协方差矩阵，描述过程噪声的协方差。它用于预测阶段，反映了模型的不确定性。

Once the “a priori” state estimate $\hat{x}_{k|k-1}$ has been predicted, the update phase comes into play. In the update phase, the “a priori” state estimate $\hat{x}_{k|k-1}$ is refined using the measurements $y_k$ recorded by the sensors. The result is the final value of the breathing parameter $\hat{x}_k$ , which is called the “a posteriori” state estimate (Equation (28)).

\hat{x}_k = \hat{x}_{k|k-1} + K_k (y_k - H \hat{x}_{k|k-1}). \quad (28)

The estimation of $\hat{x}_k$ depends on the predicted “a priori” state estimate $\hat{x}_{k|k-1}$ , the measurements registered by the different breathing sensors $y_k$ and the matrices $K_k$ and $H$ . $K_k$ is known in the Kalman filter as the optimal Kalman gain. It minimizes the “a posteriori” error covariance. A common way to calculate it is according to Equation (29).

K_k = P_{k|k-1} H^T (H P_{k|k-1} H^T + R)^{-1}. \quad (29)

This gain depends on the “a priori” estimate covariance $P_{k|k-1}$ and two model parameters ( $H$ and $R$ ). $H$ is the observation model that relates the measurements taken by the sensors $y_k$ to the state space $x_k$ (breathing parameter), as follows $y_k = H \hat{x}_k$ . It is common that previous techniques introduced in this section (peak detection, maximum-minimum detection, zero-crossings, threshold detection, frequency analysis, or wavelet transform) are used to directly estimate the respiration parameter from the measurements. In that case, the measurement space and the state space are the same. Thus, $H$ could simply be the identity matrix. If the respiration parameter (RR, for example) were not provided directly as a result of the measurements, and other parameters were given instead (such as the number of peaks, zero-crossings, etc.), matrix $H$ would contain the equations to calculate the breathing parameter from those values. Those equations were previously introduced in this section.

$R$ is the covariance of the observation noise (the noise associated with the measurements $y_k$ ). The observation noise should also follow a Gaussian distribution with zero mean and covariance $R \sim \mathcal{N}(0, R)$ . Although $H$ and $R$ can vary at each time step $k$ , it is common that they adopt a constant value.

In the update phase, the covariance is also updated to obtain the “a posteriori” estimate covariance $P_k$ according to Equation (30).

P_k = P_{k|k-1} - K_k H P_{k|k-1}. \quad (30)

As a result of the update phase, the final breathing parameter $\hat{x}_k$ is estimated, which is the output of this algorithm. However, the Kalman filter is an iterative method that recalculates $\hat{x}_k$ at each time step. Therefore, the “a posteriori” state estimate $\hat{x}_k$ at the current time step will be the previous state estimate $\hat{x}_{k-1}$ at the next time step. The same happens with the covariance since the “a posteriori” estimate covariance $P_k$ at the current time step will be the previous estimate covariance $P_{k-1}$ at the next time step. In this way, the algorithm can start a new prediction process again (Figure 33). The whole process is repeated indefinitely. The output of the system at each transition is the “a posteriori” estimate of the respiration parameters $\hat{x}_k$ .

How to implement?

Ask GPT

状态空间模型可以表示为：

\begin{cases} x_{k+1} = A x_k + B u_k + w_k \\ y_k = C x_k + D u_k + v_k \end{cases}

其中：

$x_k$ 是状态向量（呼吸参数）。
$u_k$ 是控制输入（在这个例子中可以忽略）。
$y_k$ 是观测向量（呼吸信号）。
$w_k$ 是过程噪声，假设为零均值高斯噪声，协方差为 $Q$ 。
$v_k$ 是观测噪声，假设为零均值高斯噪声，协方差为 $R$ 。

参数设置分析：

状态转移矩阵 $A$ ：假设呼吸参数在短时间内变化不大，可以设置为单位矩阵。如果有更复杂的模型，可以根据需要调整。
控制输入矩阵 $B$ ：在这个例子中没有控制输入，因此设置为零矩阵。
观测矩阵 $C$ ：假设观测值直接反映状态，因此设置为单位矩阵。如果观测值与状态有线性关系，可以调整 $C$ 。
直接传输矩阵 $D$ ：在这个例子中没有直接传输，因此设置为零矩阵。
过程噪声协方差矩阵 $Q$ ：反映模型的不确定性，通常设置为小值对角矩阵。
观测噪声协方差矩阵 $R$ ：反映观测噪声的大小，通常根据实际情况设置。
初始状态估计 $\hat{x}_0$ ：可以根据先验知识设置，或者初始化为零向量。
初始误差协方差矩阵 $P_0$ ：通常设置为单位矩阵，反映初始状态估计的不确定性。

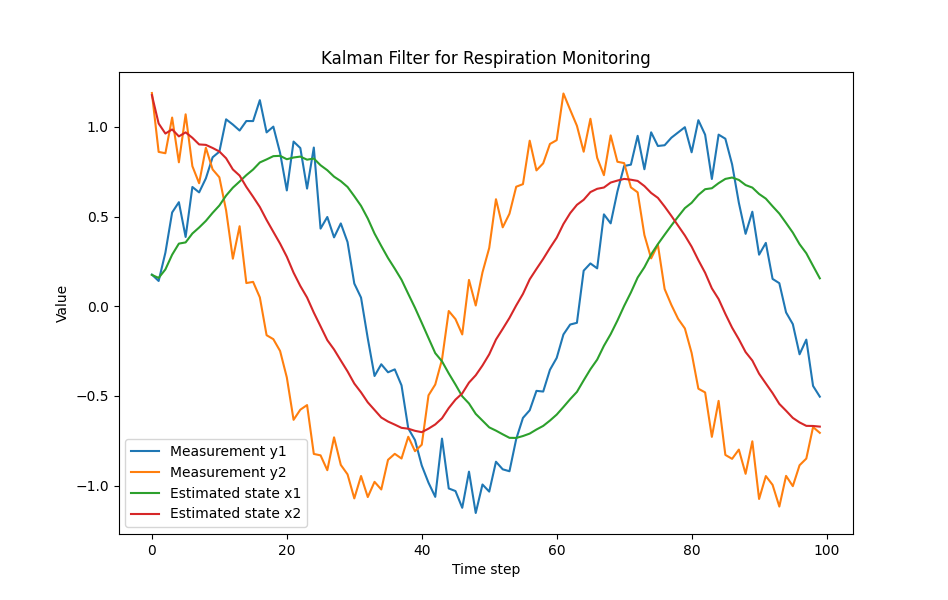
import numpy as np

# 初始化参数
A = np.eye(2)  # 状态转移矩阵，假设为单位矩阵
B = np.zeros((2, 2))  # 控制输入矩阵，假设为零矩阵
C = np.eye(2)  # 观测矩阵，假设为单位矩阵
D = np.zeros((2, 2))  # 直接传输矩阵，假设为零矩阵
Q = np.diag([1e-4, 1e-4])  # 过程噪声协方差矩阵
R = np.diag([1e-2, 1e-2])  # 观测噪声协方差矩阵
x_hat = np.zeros(2)  # 初始状态估计
P = np.eye(2)  # 初始误差协方差矩阵

# 生成模拟数据
np.random.seed(0)
y1 = np.sin(np.linspace(0, 10, 100)) + np.random.normal(0, 0.1, 100)
y2 = np.cos(np.linspace(0, 10, 100)) + np.random.normal(0, 0.1, 100)
y = np.vstack((y1, y2)).T

# 卡尔曼滤波器
x_hat_history = []
for k in range(100):
    # 预测阶段
    x_hat_minus = A @ x_hat
    P_minus = A @ P @ A.T + Q

    # 更新阶段
    K = P_minus @ C.T @ np.linalg.inv(C @ P_minus @ C.T + R)
    x_hat = x_hat_minus + K @ (y[k] - C @ x_hat_minus)
    P = (np.eye(2) - K @ C) @ P_minus

    x_hat_history.append(x_hat)

x_hat_history = np.array(x_hat_history)

# 可视化结果
import matplotlib.pyplot as plt

plt.figure(figsize=(12, 6))
plt.plot(y1, label='Measurement y1')
plt.plot(y2, label='Measurement y2')
plt.plot(x_hat_history[:, 0], label='Estimated state x1')
plt.plot(x_hat_history[:, 1], label='Estimated state x2')
plt.legend()
plt.xlabel('Time step')
plt.ylabel('Value')
plt.title('Kalman Filter for Respiration Monitoring')
plt.show()